Translated from Teploenergetika, 38 (2) 58-59 (1991) U.D.C. 621.1.016.7
The dielectric constant of dry saturated and superheated steam at subcritical pressure
Yu V Mulev
Belorussian Polytechnic Institute
The electrophysical properties of water and steam are important physical parameters, knowledge of which enables a deeper analysis to be made of internal state of a substance, opening up the possibility of optimal choice of chemical regimes for power-generating plant and development of reliable diagnostic methods for coolant. One of these parameters is the dielectric constant £ of dry saturated and superheated steam.
A study has been made of steam as a polar dielectric and formulae have been derived for calculating its dielectric constant within a range of pressures most characteristic of industrial power- generating plant.
The effect of an electrical field on a substance can be analysed by dividing it into its components. The Lorentz method is the classic approach to solving this problem.
In matter a sphere is distinguished, in the centre of which is the molecule under investigation. Diameter of the sphere is small in comparison with the distance between the faces applying the field and is considerably greater than the size of the molecule itself. The field intensity acting on this molecule can be determined from the formula:1
E = Em + E1 + E2, (1)
where Em is intensity of the mean macroscopic field in the substance; E1 is the additional field created in the centre of the sphere by the molecules disposed outside it; E2 is the additional field caused by the effect of the molecules within the sphere on the molecule under
investigation.
In the operation of power-generating plants steam can be considered as a substance in which distance between molecules is considerable in comparison with the sizes of the molecules themselves. Therefore, for the vapour state, up to a certain pressure the mutual effect of molecules one on another need not be taken into account and quantity E2 in formula (1) can be neglected.
Intensity of the mean macroscopic field in the substance can be found by the formula
Em = 4πR/(ε-1), (2)
where R is the specific electric moment of the volume.
The additional intensity created in the centre of the sphere by the molecules disposed outside it can be determined from the condition that polarisation of the sphere is similar to the appearance at its surface of an electrical charge, the density of which is proportional to polarisation. By integrating the expression determining the electrical effect on the molecule under study of the surface charge,
dE1 = dqcosθ/r2
(q = surface charge; θ = angle between direction of the electrical field and direction of the normal to the surface of the dielectric; r = radius of the sphere) an equation can be obtained which reflects the effect of the external molecules on the molecule in the centre of the sphere,
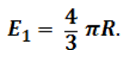 (3)
(3)
Substituting expressions (2) and (3) in (1) and making simple rearrangements, a formula can be derived relating the dielectric cosntant to the internal state of the substance:2
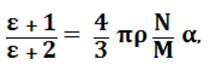 (4)
(4)
where p = density, g/m3; N = 6.022045 x 1023, Avogadro number; M = 18, molecular mass; α = 1.58 x 10-24, optical polarisability.
The main quantity characterising electrical properties is the optical polarisability. It reflects the capacity of the molecule to deform and acquire an electric moment under the effect of the external electrical field. For steam, which is a polar substance, it is necessary to take into account the dipole polarisability, determined according to the Debye theory as the ratio of the square of the dipole moment to three times the product of Boltzmnn constant and temperature T. As a result, equation (4) takes the form
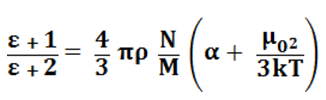 (5)
(5)
where µ = dipole moment of the molecule, taken for water as being 1.87 x 10-18 esu; k = 1.380662 x 10-16, the Boltzmann constant.
Calculations were made to check the applicability of the proposed model to steam. The following formulae were taken for comparison: the Kirkwood formula3
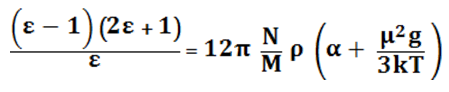 (6)
(6)
with empirical description by the Quist and Marshall factor g, taking into account the effect of field E2:4
g = [3.50+ρ(43.05+43.31ρ+17.74ρ2)T-0.32]·10-36,
subsequently, the result of calculation on the basis of this relation will be denoted ε4;
formula (6) with the empiricial equation5 for factor g:
g = [3.50+ρ(11+167ρ-94ρ2)T-0.35]·10-36 (7)
(subsequently denoted ε5);
expetimental data6 ε6;
the equation proposed as Standard by the International Association for the Properties of Steam (IAPS)7 having maximum deviation of 0.33 units ε (results denoted by ε7);
results of calculation from formula (5), ε8.
The calculations were made by computer using the instrumental language PASKAL’. The results appear in Table 1.
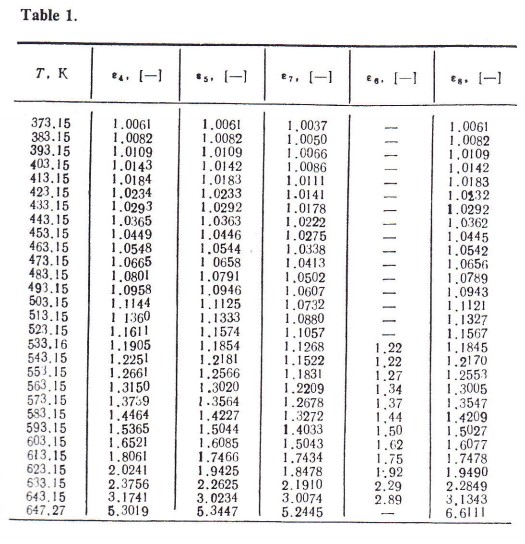
An analysis of the calculations shows that with the equations adopted the relative error
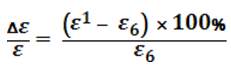 (8)
(8)
where ε1 is the magnitude of ε calculated from the respective equation; with change in temperature there is a change in the linear law. Therefore, for comparison of the formulae the mean arithmetic value of relative error is taken.
Within temperature range 523.15 — 623.15 K (point T = 643.15 K is not taken into account in calculation) the divergence between ε8 and ε6 does not exceed 0.83%, whereas that between ε7 and ε6 is 6.54%, and between ε5 and ε6 0.88%.
At lower parameters (T = 373.15 — 523.15 K), when the results of experimental studies are very sensitive to interference factors and there is a paucity of reliable experimental data, comparison is made for ε8 and ε5, and also for ε7 and ε5. For the first variant the deviation is shown in Fig. 1; for the second it is two orders higher.
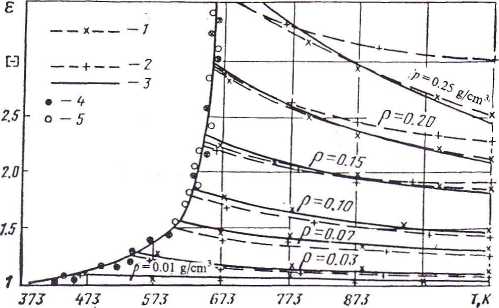
Figure 1. Dependence of dielectric constant of dry saturated and superheated steam at different densities on temperature.
1, calculation from Svistunov;6 2, from LAPS;7 3, from formula (5); 4,5, experimental data of Svistunov.6
Thus the equation put forward, reflecting the physical state of dry saturated steam, describes more precisely the dependence of dielectric constant in comparison with the known equations which contain empirical coefficients. It can be used successfully for practical calculations.
Of current interest is determination of the calculation formula for dielectric constant of superheated steam. In this journal in 1979 Professor O I Martynova reproduced the IAPS equation as an International Standard but its high error (0.33 units) cannot satisfy the requirements of investigators. The equation given by Yu M Lukashov and V N Shcherbakov in this journal in 19808 provides greater accuracy but the large number of empirical coefficients in certain cases causes difficulties in practical calculations.
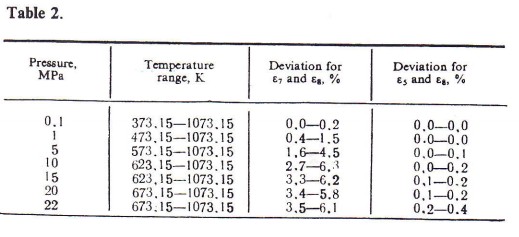
The only set of data within the range of interest to us is that of the Svistunov experiments,6 for which the results were given of dielectric constant for superheated steam on the 693, 743 and 783 K isotherms within a range of pressures from 10 to 40 MPa, and it was proposed to calculate ε from formula (6) and (7). However, the error of these data was about 2%.
Dielectric constant was calculated from the equation of the IAPS7 and from formula (5) (see Fig. 1). Comparability of the results of calculation was checked according to formula (8). The qualitative characteristics obtained are given in Table 2.
More exhaustive investigations are needed in this region, to examine not only the autonomous states of the dipole molecule of water but also its binary and ternary compounds. These investigations would be likely to reduce substantially the deviation between theoretical and experimental data. One trend could be the use of dielectric virial coefficients. But in the given stage it can be taken that the proposed equation, representing water as an assembly of autonomous electric dipoles, can be used successfully for calculating the dielectric constant of superheated steam at subcritical pressure.
References
1. B M Tareev Fizika Dielektricheskikh Materialov (Physics of Dielectric Materials), Moscow, Energoatomizdat, 1982
2. G I Skanavi Fizika Dielektrikov (Oblast' Slabykh Polei) [Physics of Dielectrics (Region of Weak Fields)],
Moscow —Leningrad, Tekhteoretizdat, 1949
3. J G Kirkwood “The dielectric polarisation of polar liquids” Journal of Chemical Physics, 1939, 7 911—925
4. AS Quist, W L Marshall “Estimation of dielectric constant of water to 800 °C” Journal of Chemical Physics, 1965, 69 3165-3167
5. E P Svistunov, B P Golubev, S N Smirnov “Measuring the dielectric constant of steam at the saturation line” Teploenergetika, 1974, 21(6) 69-70 [In English in Thermal Engineering, 1974(6) 95 — 96]
6. E P Svistunov “Investigating the dielectric constant and the electrical conductivity of steam at high parameters of state for thermal power plants”, Author’s thesis for candidate of technical science degree, Moscow, 1974
7. 0 1 Martynova “The International Table and Equation for the static dielectric constant of water and steam” Teploenergetika, 1979, 26(7) 74 — 75 [abstract in English in Thermal Engineering, 1979(7) 442-443]
8. Yu M Lukashov, V N Shcherbakov “Investigation of the dielectric constant of water at temperatures from 573 to 873 K and pressures up to 180 MPa” Teploenergetika, 1980, 27(3)
70 — 71 [In English in Thermal Engineering, 1980(3) 171 — 173]