Методика расчёта диэлектрической проницаемости аммиака в широком диапазоне параметров
Канд. техн. наук, доц. МУЛЕВ Ю. В., докт. техн. наук СМИРНОВ С. Н.
Белорусский ордена Трудового Красного Знамени политехнический институт Московский ордена Ленина и ордена Октябрьской Революции энергетический институт
Аммиак может служить перспективным теплоносителем автономных энергетических установок, является одним из компонентов водного режима теплоэнергетического оборудования и занимает в ряде технологий химического производства ведущее место. Разработка методов оперативной диагностики состояния этого вещества представляет собой актуальную задачу. Один из способов безынерционной диагностики аммиака может базироваться на измерении его диэлектрической проницаемости [1], методика расчета которой в широком диапазоне параметров отсутствует [2].
Цель настоящей работы — создание методики расчета диэлектрической проницаемости аммиака в широком диапазоне параметров, на основе которой возможны интерполяция и экстраполяция данных.
Диэлектрическая проницаемость ε аммиака теоретически может рассчитываться методами машинного эксперимента [3, 4], включающими методы Монте-Карло и молекулярной динамики. Основным рабочим параметром, используемым в таком подходе и связываемым с ε, является у, определяемый как
у=4/9πρNμ2MkT, (1)
где М – молекулярная масса;
N и k – число Авогадро и постоянная Больцмана;
μ – дипольный момент молекулы;
ρ и Т – плотность и температура вещества.
Расчет по методике, предложенной в [4], приводит к заниженным значениям е при малых величинах у и существенному превышению результатов расчета по сравнению с экспериментальными данными по диэлектрической проницаемости аммиака при у > 1,7.
Результаты расчета по уравнению Онзагера дают значение ε = 17,0 при у = 2,6, в то время как диэлектрическая проницаемость аммиака,, экспериментально установленная при соответствующих параметрах, равна 27,63.
Анализ работ по молекулярной статистике показывает, что практически все исследователи, предлагая свои теоретические модели и решения, не рассматривают реальный вид зависимости диэлектрической проницаемости вещества от параметра у, т. е. вид зависимости, построенной на основе экспериментальных данных, хотя это дает возможность получать дополнительную информацию о строении вещества, а также на ее основе, по мнению авторов, может базироваться методика расчета е в широком диапазоне параметров.
Наиболее полно экспериментальные данные по диэлектрической проницаемости аммиака представлены в [5]. Диапазон известных значений получен по плотности от 0,05 до 0,8 г/см3 и по температуре от 213,15 до 483,15 К (всего около 120 экспериментальных точек, определенных из 2 000 экспериментальных измерений). Приняты также значения по е аммиака из [6], где приведено около 20 точек. Для принятых е аммиака температурный интервал составил 10 К- По плотности — 0,1 г/см3. Значения плотности приведены в указанных источниках.
Диэлектрическая проницаемость аммиака из [5, 6] использована только для представленных табличных величин. Данные для междушагового пространства в последующих расчетах исключались.
В результате расчета параметра у и применения соответствующего значения диэлектрической проницаемости аммиака, полученного из экспериментальных исследований, на рис. 1 изображены точки зависимости ε = f(у). В диапазоне у = 0,65—3,0, соответствующем жидкому состоянию вещества, зависимость диэлектрической проницаемости от параметра у близка к линейной. Небольшой разброс (не превышающий нескольких процентов) не связан с температурой или плотностью и его следует отнести к погрешности эксперимента.
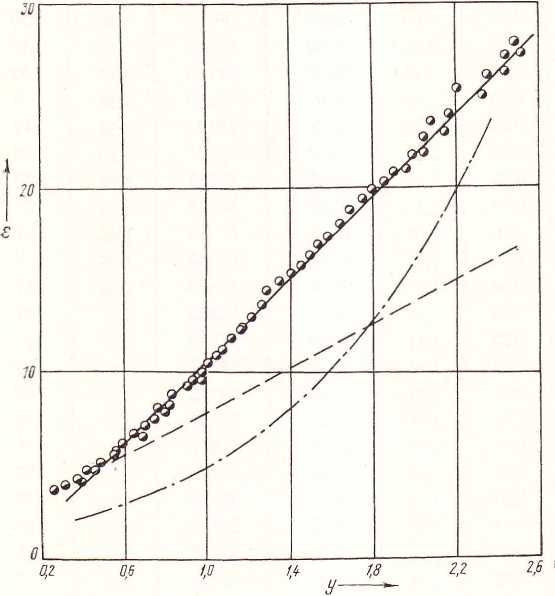
Рис. 1. Зависимость диэлектрической проницаемости аммиака от параметра у:
— - расчет по (2); - - - - по уравнению Онзагера; — • — — по [4]; ▄ — экспериментальные точки из [5, 6]
Таблица 1
Результаты аппроксимации зависимости диэлектрической проницаемости аммиака
от параметра у

* Значение отклонений приведены в абсолютных единицах ε.
Таблица 2
Значения диэлектрической проницаемости аммиака при плотностях 0,90, 0,95
и 1,0 г/см3
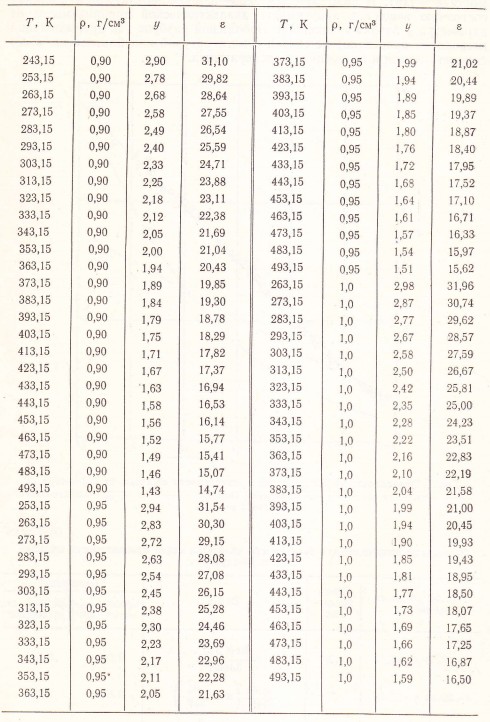
Линейность зависимости ε = f(у) представляет возможность расчета диэлектрической проницаемости аммиака по плотности и температуре практически во всем диапазоне существования жидкого состояния. Использование в (1) в качестве переменного только отношения р/Т и линейность зависимости ε = f(у), как будет показано ниже, при одновременном увеличении р и Т и удержании у в обозначенных рамках (у = 0,65—3,0) позволяют провести экстраполяцию в неисследованные ■области параметров.
Для получения аппроксимационного уравнения для жидкого состояния аммиака из рассмотрения исключены данные со значениями у > 3. Для аппроксимации линейного участка принята прямая линия. Ее параметры определены методом наименьших квадратов [7]. Расчеты приведены для у с учетом и без учета составляющей поляризации смещения. В результате имеем уравнения, представленные в табл. 1. Видно, что учет поляризации смещения приводит к отклонению получаемой зависимости от линейной. Поэтому в расчетах использование аппроксимационного уравнения (2) предпочтительнее.
Экстраполяцией на основе уравнения (2) получены значения диэлектрической проницаемости аммиака в неисследованной области высоких плотностей (табл. 2).
Таблица 3
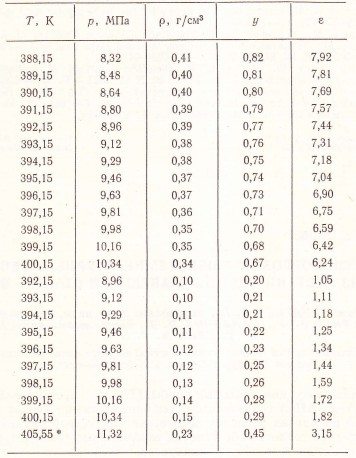
* Параметры критической точки
Необходимо знание диэлектрической проницаемости аммиака в околокритической области и критической точке, где методика экспериментальных исследований особенно трудоемка.
Как видно из рис. 1, зависимость г от параметра у на начальном участке также линейна. Аппроксимация зависимости для диапазона у = 0—0,65 проведена на основе данных из [5, 6] по изложенной выше методике. Полученные уравнения приведены в табл. 1.
Дополнительные расчеты показали, что уравнение (4) удовлетворительно описывает зависимость ε при изменении у от 0,2 до 0,65. При более низких значениях у целесообразнее использование методики расчета диэлектрической проницаемости аммиака на основе вириальных коэффициентов.
Использование уравнений (4) и (2) позволяет получить значения диэлектрической проницаемости аммиака в околокритической области и критической точке (табл. 3). Соответствующие данные по плотности аммиака приняты из [8].
Таким образом, предложенная методика расчета, основанная на линейности экспериментальной зависимости е от параметра у, позволяет рассчитывать диэлектрическую проницаемость аммиака в широком диапазоне параметров.
ЛИТЕРАТУРА
1. Смирнов С. Н. Расчетно-экспериментальное определение диэлектрической проницаемости сжатых газов, газовых смесей и таблицы для автоматизации контроля теплофизических свойств в энергетике: Автореф... докт. техн. наук.— М.: МЭИ, 1986.— 47 с.
2. Синтез аммиака/Л. Д. Кузнецов, Л. М. Дмитренко, П. Д. Рабина и др.— М.: Химия, 1982.— 296 с.
3. Ю х н о в с к и й И. Р., Г о л о в к о М. Ф. Статистическая теория классических равновесных систем.— Киев: Наукова думка, 1980.— 372 с.
4. Patey G. N. An integral equation theory tor the dence dipolar hard-sphere fluid// Mol. Phys., 1977,—Vol. 34,—N 2,—P. 427—440.'
5. В u b a c k M., Harder W. D. The static Dielectric Constant of Ammonia to High Pressures and Temperatures. S. Computer Assisted Data Evaluation.— Berichte der Bunsen.— Gesellschaft, Bd. 81, Nr, 6, 1977.— P. 603—614.
6. Dannhauser W., Bähe L. W. Dielectric Constant of hydrogen bouded liquids. 3. Superhead alcohols//J. Chem. Phys., 40, N 10, 1964.— P. 3058—3066.
7. Гусак А. А. Элементы методов вычислений.— Мн.: Изд-во БГУ, 1982.— 166 с.
8. Теплофизические свойства аммиака / И. Ф. Голубев, В. П. Кияшова, И. И. Перельштейн и др.— М.: Изд-во стандартов, 1978.— 264 с.
Представлена научно-техническим Поступила 6.06.1990. После
советом кафедры ВТ и СУ доработки 2.10.1990

