Канд. техн. наук. доц. МУЛЕВ Ю. В.
Белорусская государственная политехническая академия
Электрофизические свойства могут быть положены в основу создания надежных безынерционных систем измерения и контроля параметров водного теплоносителя как при различных теплофизических экспериментах, так и в промышленных условиях диагностики состояния водного теплоносителя по всему тракту движения рабочего тела энергетического оборудования. По измеряемым макроскопическим величинам электрофизических параметров возможен переход к отдельным молекулярным константам, к получению информации о строении вещества.
Основные исследования воды и водяного пара энергетических параметров в большинстве случаев ограничивались радиочастотным диапазоном. Это обусловило существование уравнения, принятого Международной ассоциацией по свойствам воды и водяного пара, для статической диэлектрической проницаемости [1]. При высоких и сверхвысоких частотах вода энергетических параметров исследовалась только в отдельных работах.
Методики расчета электрофизических свойств водного теплоносителя при различных частотах воздействующего электромагнитного поля отсутствуют, хотя сведения о поведении вещества при различных частотах намного актуальнее и информативнее по сравнению со статической диэлектрической проницаемостью.
В настоящей работе рассмотрено поведение таких параметров водного теплоносителя в диапазоне от звуковых до сверхвысоких частот как диэлектрическая проницаемость и тангенс угла диэлектрических потерь-— величин, на основе которых несложно переходить к другим различным характеристикам электрофизических свойств.
В условиях работы энергетического оборудования к теоретическому исследованию воды и водяного пара в полной мере может быть применена физика диэлектриков.
Для описания электрофизических свойств веществ в широком частотном диапазоне одной из наиболее известных является формула Дэвидсона— Коула [1]
*ε= ε∞+ εs+ ε∞(1+jωτ)β,
из которой при β = 1 несложно получить
ε'= εs- ε∞1+ω2τ2+ ε∞ (1)
и
ε''= (εs- ε∞)ωτ1+ω2τ2 , (2)
где ε' и ε'' — действительная и мнимая части комплексной диэлектрической проницаемости ε, соответственно отражающие емкостную и активную составляющие;
εs, ε∞ - статическая и высокочастотная диэлектрические проницаемости;
ω = 2πf – круговая частота;
f – частота воздействующего электромагнитного поля;
τ – диэлектрическая релаксация;
β – параметр, характеризующий распределение по времени релаксации.
Из анализа данных по электрофизическим свойствам воды, которые представлены в [3], можно заключить, что β ≅ 1. Аналогичный вывод следует из [4], где проведены исследования диэлектрических свойств воды при нормальной температуре. Поэтому можно предположить, что для водного теплоносителя применимы уравнения (1) и (2), которые носят название уравнений Дебая. Для их использования в расчете электрофизических характеристик водного теплоносителя необходимо определить методики расчета составляющих этих уравнений.
Статическая диэлектрическая проницаемость водного теплоносителя в жидком состоянии может быть рассчитана по методике, предложенной в [5], и основана на однозначности зависимости εs от параметра поляризации Y (рис. 1), определяемого по уравнению
Y=4/9πNAρ/Mμ2kT, (3)
где μ — дипольный момент изолированной молекулы;
NA и k —число Авогадро и постоянная Больцмана;
М — молекулярный вес;
ρ и Т — плотность и температура.
Уравнения, связывающие εs и Y, приведены в табл. 1.
Для расчета статической диэлектрической проницаемости сухого насыщенного и перегретого водяного пара докритической плотности может быть применено уравнение Клаузиуса — Моссотти [6]:
εs-1εs+2=4/3πNAρ/M(α+μ23kT), (4)
где α – деформационная поляризуемость молекулы.
Таблица 1

* ϭ – среднеквадратичное отклонение.
Высокочастотную диэлектрическую проницаемость водного теплоносителя, обусловленную деформационной составляющей поляризации, наиболее рационально определять из поляризации льда по
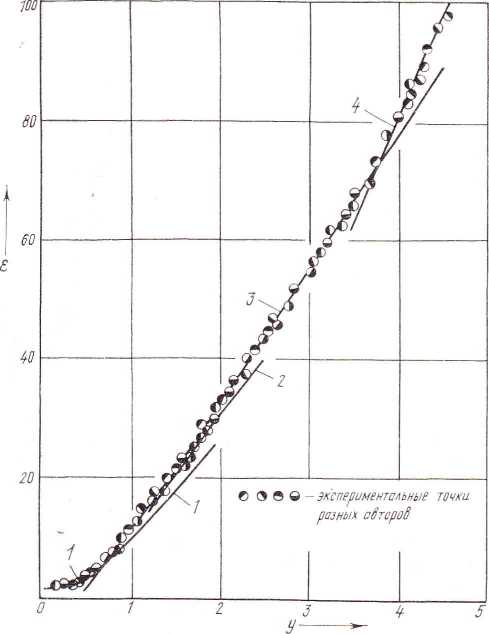
Рис. 1. Зависимость диэлектрической проницаемости водного теплоносителя в жидкой фазе от параметра поляризации У:
1 — расчет по (5); 2 — по (6); 3 — по (7); 4 — по (8)
методике, предложенной в [7, 8] и расширенной применительно к энергетическим параметрам воды в [9]; ε∞ вычисляется из уравнения
ε∞-1ε∞ +2 ∙ Мρ=Pj, (9)
где Pj - поляризация, принимаемая для водного теплоносителя постоянной и равной 8,4 см3/моль.
Время диэлектрической релаксации водного теплоносителя определяем из уравнения [10]
τ = (2,61μ/T + 0,32) 10-12, (10)
где μ — коэффициент динамической вязкости.
Таким образом, используя уравнения (5) — (10), на основе (1) рассчитываем значение диэлектрической проницаемости водного теплоносителя в широком частотном диапазоне (рис. 2а). Видно, что ε' воды имеет постоянное значение. Существенное уменьшение значений наступает после
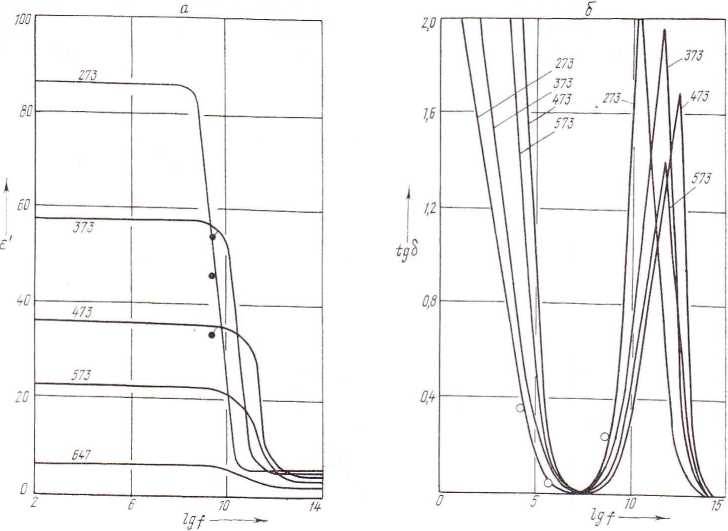
Рис. 2. Зависимость диэлектрической проницаемости (а) и тангенса угла диэлектрических потерь (б) водного теплоносителя в жидком насыщенном состоянии и при нормальной температуре от частоты воздействующего электромагнитного поля:
• — экспериментальные точки из [8]; О — из [12]
частот порядка (1—10) · 1010 Гц. Такое падение ε' обусловлено снижением ориентационной поляризации, когда диполи вещества не успевают следовать за изменением направления электрического поля. Начало такого спадания смещается с ростом температуры в сторону повышения частоты электромагнитного поля.
При анализе активной составляющей комплексной диэлектрической
проницаемости *ε наиболее часто используют величину тангенса угла диэлектрических потерь, определяемую при наличии свободных носителей электрических зарядов выражением [11, 12]
tg δ = ε''/ε' + tg ϭ, (11)
где ε''/ε' — диэлектрические потери, обусловленные ориентационной составляющей поляризации;
tg ϭ — диэлектрические потери, связанные со свободными носителями зарядов.
Применительно к водному теплоносителю уравнение (11) может быть представлено в виде [13]
tg δ= (εs- ε∞)ωτεs+ ε∞ω2τ2+ xεsε∞ω , (12)
где х—удельная электропроводность раствора, которая при условии низких концентраций солей у воды в основном обусловлена собственной диссоциацией.
Из выражения для ориентационных потерь можно видеть, что с ростом частоты эти потери возрастают, достигая при определенном значении f максимального значения, и при дальнейшем повышении частоты воздействующего электромагнитного поля падают.
Потери, обусловленные сквозной проводимостью, из-за снижения подвижности ионов с ростом частоты снижаются.
Удельную электропроводность х при диссоциации можно представить как
x= Kω(λH++λOH-), (13)
где Kω — ионное произведение воды;
λH+ и λOH- — эквивалентные проводимости собственных ионов воды, н он
Используя предыдущие уравнения расчета величин, входящих в (12) и выражение (13), можно определить значения тангенса угла диэлектрических потерь для водного теплоносителя (рис. 26).
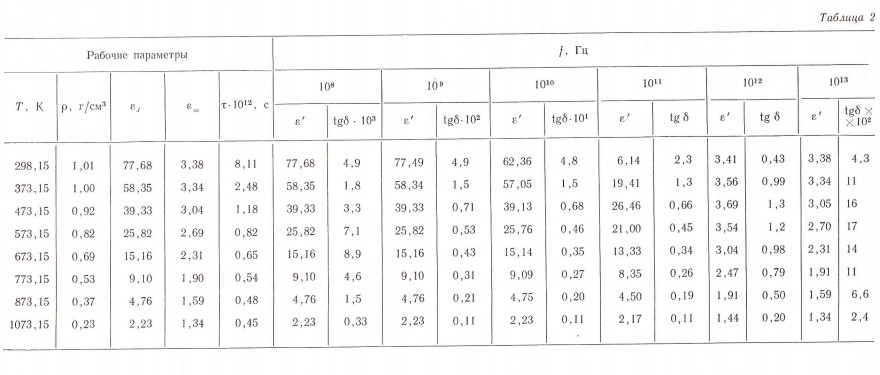
На основе предложенной методики рассчитаны значения диэлектрических характеристик воды при температурах от 298 до 1073 К (табл. 2).
При разработке диагностических систем актуально определение рабочей частоты, при которой значение тангенса угла диэлектрических потерь минимально. Формулу для определения f(tg δmin) получим путем приравнивания выражений для ориентационной и проводимостной диэлектрических потерь из (12)
(εs- ε∞)ωτεs+ ε∞ω2τ2= xεsε∞ω . (14)
Преобразуя (14), можно записать
f = 14πε∞τ ∙ xεsτ+ πε0(εs- ε∞) , (15)
где f определяет для водного теплоносителя частоту, при которой тангенс угла диэлектрических потерь минимален.
Таким образом, уравнения (1) —(15) позволяют рассчитывать электрофизические свойства водного теплоносителя в широком диапазоне параметров состояния при различных частотах воздействующего электромагнитного поля.
ЛИТЕРАТУРА
1. Мартынова О. И. Международные таблицы и уравнения для статической диэлектрической константы воды и водяного пара//Теплоэнергетика.—1979.— № 7.— С. 74—75.
2. Борисова М. Э., Койков С. Н, Физика диэлектриков.— Л.: ЛГУ.—1979.—
240 с.
3. Ахадов Я. Ю. Диэлектрические свойства чистых жидкостей.— М.: Изд-во стандартов.—1971.—420 с.
4. Dielectric spectra of some common solvents in the microwave region. Water and lower alcohols /J. Barthel, К. Bachhuber, R. Buchner, H. Hetzenauer//Chem. Phys. Leiters.—1990,—V. 165,—№ 4,—P. 369—373.
5. M y л e в Ю. В., Смирнов C. H. Методика расчета диэлектрической проницаемости воды и водяного пара в широком диапазоне параметров / Тез. Междунар. симп.
Теплофизика-90».— Обнинск, 1990.— С. 130—131.
6. М у л е в Ю. В. Методика расчета диэлектрической проницаемости сухого насыщенного и перегретого водяного пара докритической плотности//Теплоэнергетика.— 1991.—№ 2,—С. 51—52.
7. Любимов Ю. А., Набоков О. А. Об определении диэлектрической проницаемости на «бесконечно большой частоте»//Журнал физ. химии.—1984.— № 9.—• С. 2230—2238.
8. Набоков О. А., Любимов Ю. А. Диэлектрическая релаксация воды вдоль кривой сосуществования//Вестник МГУ. Химия.— Деп. ВИНИТИ.—1985.—№ 4597.— Деп.— 19 с.
9. Му лев 10. В. К вопросу расчета высокочастотной диэлектрической проницаемости водного теплоносителя//Энергетика... (Изв. высш. учеб, заведений).—1992.— № 2,—С. 99—101.
10. Мулев Ю. В., Смирнов С. Н. Методика расчета времени диэлектрической релаксации водного теплоносителя в широком диапазоне параметров состояния // Энергетика... (Изв. высш. учеб, заведений).—1992.— № 1.— С. 115—118.
11. Усиков С. В. Электрометрия жидкостей// Л.: Химия, 1974.—144 с.
12. Хиппель А. Р. Диэлектрики и их применение.— М.: Госэнергоиздат, 1959.— 336 с.
13. Мулев Ю. В. Методика расчета электрофизических свойств водного теплоносителя в широком диапазоне параметров состояния при различных частотах//Тез. докл. на Всесоюз. конф.: Измерение и контроль при авт. произв. процессов.— Барнаул.— 1991,—2 с.
Представлена НТС ВТ и СУ Поступила 24.01.1992