Канд. техн. наук, доц. МУЛЕВ Ю. В., докт. техн. наук СМИРНОВ С. Н,
Белорусская государственная политехническая академия Московский ордена Ленина и ордена Октябрьской Революции энергетический институт
Время диэлектрической релаксации τ является одним из основных информационных параметров, позволяющих исследовать тепловые движения молекул полярной жидкости. В применении к водному теплоносителю его знание позволяет уменьшить количество недостающих параметров в уравнении Дебая, которое, в свою очередь, открывает возможность описания электрофизических свойств воды в широком диапазоне воздействующих частот электромагнитных полей. В научном аспекте время диэлектрической релаксации — самостоятельный параметр, содержащий информацию как о состоянии отдельных молекул, так и межмолекулярном взаимодействии в исследуемом веществе.
В настоящей работе предложена методика расчета времени диэлектрической релаксации водного теплоносителя в широком диапазоне параметров состояния.
При исследовании времени диэлектрической релаксации в большинстве случаев используют корреляционную функцию переориентации, диполя с моментом μ, представляющую собой усовершенствованный вид модели Онзагера [1, 2]:
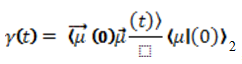(1)
где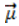 
(t) – составляющая временного фактора.
Для связи функции (1) с макроскопическими параметрами наиболее известно соотношение [3]
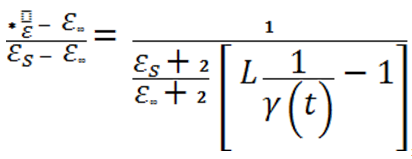(2)
где L [... ] — определяет оператор преобразования Фурье— Лапласа;
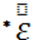– комплексная диэлектрическая проницаемость;
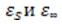- диэлектрические проницаемости вещества, измеренного на низких и сверхвысоких частотах, когда имеет место только деформационная поляризация.
Если исходить из традиционно принятой экспоненциальной зависимости
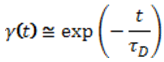(3)
то связь между временем релаксации τ и молекулярным временем корреляции τD определяется выражением [3]
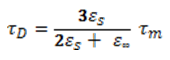(4)
Недостатком такого подхода, как показано в [4, 5], является принятое представление исследуемой модели с разной диэлектрической проницаемостью анализируемой сферы и матричной среды.
Более корректен подход, где сфера диэлектрического образца расположена в бесконечной диэлектрической среде с тем же значением комплексной диэлектрической проницаемости. Для такого случая в [2] предложено соотношение
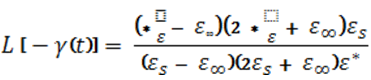(5)
исходя из которого в предположении (3) можно получить
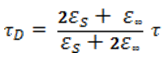(6)
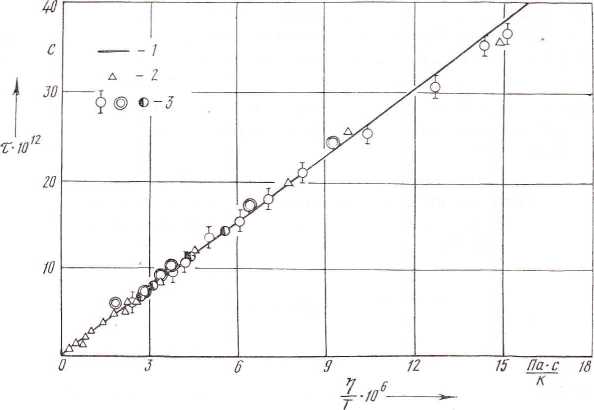
Рис. 1. Зависимость диэлектрической релаксации воды от параметра η/Т:
1 — расчет по (8); 2 — данные из [11]; 3 — экспериментальные данные разных авторов из [9]
Принятие для последующего анализа формулы (6) не снимает, однако, необходимости в определении корреляционной функции γ(t). В [6] проведены расчеты γ(t) на основе экспериментальных данных, как при додисперсных частотах, так и в инфракрасной области спектра.
Отсутствие успеха в этой работе обусловлено как невысокой точностью данных по диэлектрическим свойствам веществ, так и несовершенством принимаемых моделей ориентационных движений молекул конденсированной среды.
В [7] описана модель столкновительной диффузии, где применена теория газоподобных столкновений к плотным конденсированным средам, что вызывает сомнение в корректности результатов последующих расчетов. В модели непрерывной диффузии [6], как это отмечено в [8], вращательное броуновское движение рассмотрено как предельный случай столкновительной модели, когда частота столкновений значительно больше частоты свободных вращений. Обе эти модели к настоящему времени не могут быть реализованы в методике расчета диэлектрической релаксации водного теплоносителя, и поэтому нами предлагается несколько иной вариант решения этой проблемы.
Из соотношения, предложенного Дебаем и связывающего время релаксации с молекулярными постоянными,
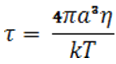(7)
где k — постоянная Больцмана, очевидно, что при постоянстве радиуса молекулы а время релаксации зависит от отношения вязкости η к температуре Т.
Нами прелагается рассмотреть зависимость времени диэлектрической релаксации т от отношения η/Т, используя результаты экспериментальных исследований.
По данным [9], где собраны результаты наиболее известных экспериментов, время диэлектрической релаксации воды исследовалось разными авторами при температурах от 273 до 373 К. В [10] приведены результаты экспериментальных исследований т воды при температурах от 273 до 305 К и в состоянии переохлаждения. Для разработки систем контроля и измерений в промышленных условиях теплоэнергетических установок, а также при проведении ряда химико-технологических процессов возникает необходимость исследования диэлектрических свойств воды при температурах выше 373 К. Для таких условий известны исследования по времени релаксации воды только в одной работе [11].
Вид зависимости времени релаксации от отношения η/Т определен на основе экспериментальных данных из [9—11]. Значения вязкости для воды при температуре выше 273 К принимались из [12], для переохлаждения воды—из [13] .
Созданный массив состоял из 55 экспериментальных точек (рис. 1). При этом из полученного объема данных исключены три точки авторов Конна и Сайса при температурах 353, 363 и 373 К, так как различие в их значениях по сравнению с данными [9—11] превышало 45 % и эти точки отнесены к промахам.
Из представленного на рис. 1 массива данных очевидно, что полученные точки исследуемой зависимости образуют прямую линию. При этом отсутствуют неоднозначности, связанные с температурой или вязкостью. Это дает возможность определять время релаксации воды в широком диапазоне параметров состояния, основываясь на значении отношения η/Т, однозначно связанного с τ.
Полученная зависимость аппроксимирована на ПЭВМ 1ВМ РБ/АТ с использованием инструментального языка Паскаль методом наименьших квадратов прямой линией вида
τ = [ (2,61 η/Т) + 0,32] · 10-12 , (8)
Среднеквадратичное отклонение результатов расчета по (8) от экспериментальных данных составило:
для диапазона η/Т ·106 от 0 до 2 Па·с/К – 0,04·10-12 с,
от 2 до 6,6 – 0,6·10-12 с,
от 6,6 до 15,2 – 0,8·10-12 с;
На основании проведенной аппроксимации возможно получение значений времен релаксации в неисследованных областях. Так, например, принимая значения вязкости воды из [14] при соответствующих температурах и давлениях, найдены значения τ кипящей воды энергетических параметров (табл. 1). Сравнение полученных результатов с опытными данными из [11], погрешность которых по оценке авторов составляет 7 %, показывает, что расхождение расчета и эксперимента сопоставимо с точностью результатов исследований.
Таким образом, предложенная методика расчета времени релаксации,, основанная на линейности и однозначности этого параметра от соотношения η/Т и достаточно несложная в применении, может быть использована для интерполяции и экстраполяции данных для определения диэлектрических параметров воды в широком диапазоне параметров состояний.
Таблица 1
Значения диэлектрической релаксации воды энергетических параметров
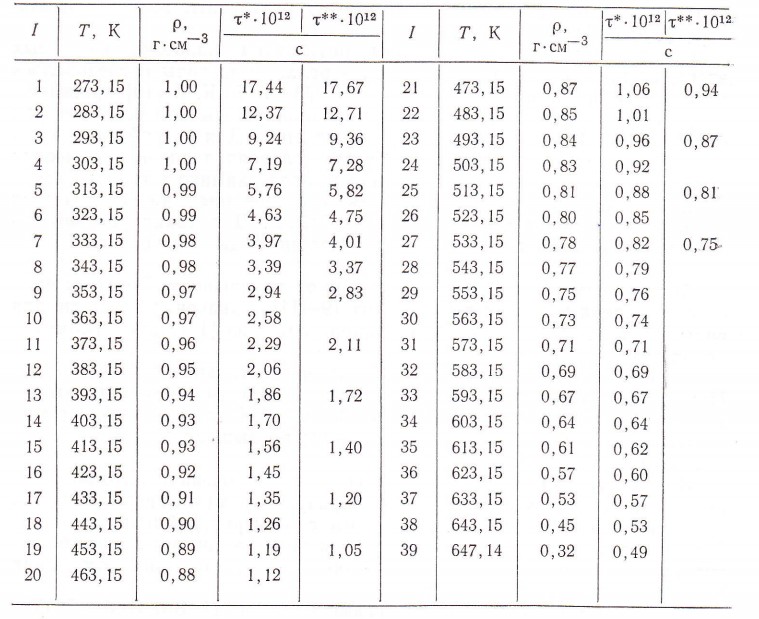
* Расчет по предложенной методике
** Экспериментальные данные из [11].
ЛИТЕРАТУРА
1. G 1 arum S. Н. Dielectric relaxation of polar liquids//J. Chem. Phys.—1960.— V. 33.—№ 5.—P. 1371 — 1375.
2. N ее T. W., Zwanzig R. Theory of dielectric relaxation in polar liquids// J. Chem. Phys.—1970,—V. 52,—№ 12,—P. 6353—6363.
3. С о 1 e R. H. Correlation function theory of dielectric relaxation//J. Chem. Phys.— 1965,—V. 42,—№ 3.—P. 637—643.
4. Hill N. E. The theory of complex permittivity//J. Phys. C: Solid. State Phys.— 1972,—V. 5,—№ 4,—P. 415—424.
5. Kivelson D, Ma ddin P. Theory of dielectric relaxation // Mol. Phys.—1975.—■ V. 30,—№ 6.—P. 1749—1780.
6. Local coherence in the orientational dynamics of highly polar liquid / A. Gerchel, I. Dimicoli, J. Jaffre, A. Riou//Mol. Phys.— 1977,—V. 33,—№ 2,—P. 527—541.
7. G о r d о n R. G. On the rotational diffusion of molecules//J. Chem. Phys.—1966.— V. 44,—№ 5.— P. 1830—1836.
8. H а б о к о в О. А. Исследование диэлектрических свойств воды вдоль кривой сосуществования: Дис. ... канд. физ.-мат. наук.— М.: МГУ.—1986.—169 с.
9. А х а д о в Я- Ю. Диэлектрические свойства чистых жидкостей.— М.: Изд-во стандартов.—1972.—412 с.
10. Bertolini D., Cassettari М., Balvetti G. The dielectric relaxation time- c: supercooled water // J. Chem. Phys.—1982.— V. 76.— № 6.— P. 3285—3290.
11. Набоков О. А., Любимов Ю. А. Диэлектрическая релаксация воды и во- .дородные связи в воде//Хим. физика.—1988 —Т. 7.— № 5.— С. 634—640.
12. ГСССД 6—89. Вода. Коэффициент динамической вязкости при температурах 0,..800°С и давлениях от соответствующих разреженному газу до 300 МПа. Таблицы стандартных справочных данных // Свойства материалов и веществ. Вода и водяной пар.—'М.: Изд-во стандартов.—1990.— Вып. 1.— С. 15—37.
13. Осипов Ю. А., Желез ный Б. В., Бондаренко Н. Ф. Сдвиговая вязкость воды, переохлажденной до —35°С//Журн. физ. химии.—1977.— Т. 51.— Вып. 5.— С. 1264—1265.
14. Ривкин С. Л., Александров А. А. Теплофизические свойства воды и водяного пара.— М.: Энергия, 1980.—424 с.
Представлена НТС ВТ и СУ Поступила 8.08.1991
